昨天小六、維尼、小籠包與小范等小豬四兄弟 來找我討論微積分, 但是在反函數的部份我好像說的不太清楚, 心裡總是覺得怪怪的, 就找了些資料再做些整理.
來找我討論微積分, 但是在反函數的部份我好像說的不太清楚, 心裡總是覺得怪怪的, 就找了些資料再做些整理.
反函數( Inverse Function )
簡單來說, 給定一個函數 f(x), 可以找到另一個函數g, 將 f(x) 當作g的自變數, g( f(x) ) = x.
原本的 f 函數是將 x 代入函式運算後得到一個值, 我們先假設是 y ; 現在將 y 代入 g 這個函數運算後可以得到原來的 x, 便可以稱g 是 f 的反函數.
有沒有點感覺了呢? 好吧~再舉個很爛的例子, 假設將一頭豬塞進機器可以做出香腸, 豬就是 x , 機器就是 f , 香腸就是 y ; 如果今天有另一台機器可以將香腸塞進去, 然後生出原來那隻小豬的話(乖乖嚨低冬....真是太神奇了), 這台機器就可以叫做是 f 的反函數囉!
假設現在已經有點概念了, 再來看看一些較為正規的定義, 在Larson這本教材上好像有個定理是這樣說的:
Theorem5.7
1. A function has an inverse function if and only if it is one-to-one.
2. If F is strictly monotonic on its entire domain, then it is one-to-one and therefore has an inverse function.
根據我未通過任何英檢的外語程度來翻的話就是:
1. 一個函數具有1-1的關係與這個函數具有反函數這兩個敘述是等價的
2. 如果一個函數在它的定義域裡是strictly monotonic , 它便具有1-1的對應關係而且有反函數.
這邊可能稍微要為那些平常不念書或是基礎沒打好的人解釋一下一些專有名詞啦! 我承認我以前也是前述集合中的一個元素啦 XD.
1-1 (one-to-one)是什麼阿?
函數的對應關係有一對一和多對一, 但絕沒有一對多. 一對一的意思就是將一個自變數 x 代入函數可以在值域得到一個且唯一對應的值; 多對一則是將幾個不同的 x 帶入函數運算後都會得到同一個對應的值, 譬如 f = ( x )( x ) , 不管 x = 2 或是 x =(-2) 代入函數運算後都會得到 4 這個對應值, 這就是多對一.
等價是什麼阿?
要解釋這個真的有點頭大唉~基本上集合上的二元關係若滿足反身性( Reflexivity )、對稱性( Reflexivity ) 和傳遞性( Transitivity ) 就可以稱這個關係是定義在某集合上的等價關係, 目前先將它當作等於的關係好了.
Monotonic是什麼鬼阿?
在MathWorld中定義為:
A function which is either entirely nonincreasing or nondecreasing. A function is monotonic if its first derivative (which need not be continuous) does not change sign.
也就是一個函數必須是nonincreasing 或 nondecreasing 的樣子, 數學就愛用這些文謅謅的語法, 用圖來看一下就懂了,
在圖形的左邊是持續遞增的狀態, 就算圖形中間的部份沒有遞增, 仍是持平的狀態並沒有遞減. 所以這是一個nondecreasing的函數圖形.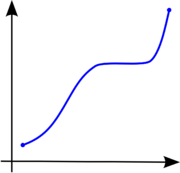
反之, 下圖則為nonincreasing的函數圖形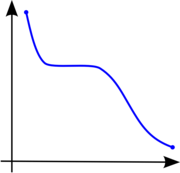
當然還有無法歸類為上兩者的函數圖形
看完上面一對堆囉哩八縮的敘述是不是對於反函數有比較多的認識了, 沒有的話直接按 上一頁不用浪費時間繼續看下去啦!
上一頁不用浪費時間繼續看下去啦!
Larson的書上有提到尋找反函數的方式, 其實也不過就是將 y = .....這樣的函數型態改寫成 x=.....的型態, 然後將轉換後的 x 和 y 作個俏皮地交換,  交換的用意是表示自變數經由函數對應到值域後會在經由反函數對應回來到自己. 最後兩項規則只是為了驗證並使求出的反函數更加嚴謹.
交換的用意是表示自變數經由函數對應到值域後會在經由反函數對應回來到自己. 最後兩項規則只是為了驗證並使求出的反函數更加嚴謹.

有興趣的人可以再看一下Wiki上的例子:
若給定一函數x → 3x + 2,則其反函數為x → (x−2) / 3。這通常寫成:
一般而言,當f(x)為一任意函數,且g為其反函數,則g(f(x)) = x且f(g(x)) = x。換句話說,一反函數會取消原函數的作用。在上述例子,可以證明f−1確為反函數,以將(x − 2) / 3代入f的方式,如此
- 3[ (x − 2) / 3 ]+ 2 = x
橘色反白的部份是原函數 f 的 x .
以上所有寫作材料參考如下:
[1] MathWorld
[2] Wikipedia
[3] Calculus 8th Edition, Larson
附錄:微積分公式表(PDF格式)
呼~寫了3小時終於寫完了, 希望沒甚麼太大的問題, 關於出處以及文章有任何問題歡迎留言討論喔! 請大家多多指教.

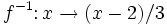



 留言列表
留言列表